Physical principles




Solar radiation pressureedit

Many people believe that spacecraft using solar sails are pushed by the Solar winds just as sailboats and sailing ships are pushed by the winds across the waters on Earth. But Solar radiation exerts a pressure on the sail due to reflection and a small fraction that is absorbed.

The momentum of a photon or an entire flux is given by Einstein's relation:

p = E/c

where p is the momentum, E is the energy (of the photon or flux), and c is the speed of light. Specifically the momentum of a photon depends on its wavelength p = h/λ

Solar radiation pressure can be related to the irradiance (solar constant) value of 1361 W/m2 at 1 AU (Earth-Sun distance), as revised in 2011:

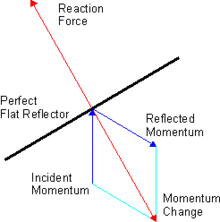
  • perfect absorbance: F = 4.54 μN per square metre (4.54 μPa) in the direction of the incident beam (an inelastic collision)
  • perfect reflectance: F = 9.08 μN per square metre (9.08 μPa) in the direction normal to surface (an elastic collision)

An ideal sail is flat and has 100% specular reflection. An actual sail will have an overall efficiency of about 90%, about 8.17 μN/m2, due to curvature (billow), wrinkles, absorbance, re-radiation from front and back, non-specular effects, and other factors.

The force on a sail and the actual acceleration of the craft vary by the inverse square of distance from the Sun (unless extremely close to the Sun), and by the square of the cosine of the angle between the sail force vector and the radial from the Sun, so

F = F0 cos2 θ / R2 (ideal sail)

where R is distance from the Sun in AU. An actual square sail can be modeled as:

F = F0 (0.349 + 0.662 cos 2θ − 0.011 cos 4θ) / R2

Note that the force and acceleration approach zero generally around θ = 60° rather than 90° as one might expect with an ideal sail.

If some of the energy is absorbed, the absorbed energy will heat the sail, which re-radiates that energy from the front and rear surfaces, depending on the emissivity of those two surfaces.

Solar wind, the flux of charged particles blown out from the Sun, exerts a nominal dynamic pressure of about 3 to 4 nPa, three orders of magnitude less than solar radiation pressure on a reflective sail.

Sail parametersedit

Sail loading (areal density) is an important parameter, which is the total mass divided by the sail area, expressed in g/m2. It is represented by the Greek letter σ.

A sail craft has a characteristic acceleration, ac, which it would experience at 1 AU when facing the Sun. Note this value accounts for both the incident and reflected momentums. Using the value from above of 9.08 μN per square metre of radiation pressure at 1 AU, ac is related to areal density by:

ac = 9.08(efficiency) / σ mm/s2

Assuming 90% efficiency, ac = 8.17 / σ mm/s2

The lightness number, λ, is the dimensionless ratio of maximum vehicle acceleration divided by the Sun's local gravity. Using the values at 1 AU:

λ = ac / 5.93

The lightness number is also independent of distance from the Sun because both gravity and light pressure fall off as the inverse square of the distance from the Sun. Therefore, this number defines the types of orbit maneuvers that are possible for a given vessel.

The table presents some example values. Payloads are not included. The first two are from the detailed design effort at JPL in the 1970s. The third, the lattice sailer, might represent about the best possible performance level. The dimensions for square and lattice sails are edges. The dimension for heliogyro is blade tip to blade tip.

Type σ (g/m2) ac (mm/s2) λ Size (km2)
Square sail 5.27 1.56 0.26 0.820
Heliogyro 6.39 1.29 0.22 15
Lattice sailer 0.07 117 20 0.840

Attitude controledit

An active attitude control system (ACS) is essential for a sail craft to achieve and maintain a desired orientation. The required sail orientation changes slowly (often less than 1 degree per day) in interplanetary space, but much more rapidly in a planetary orbit. The ACS must be capable of meeting these orientation requirements. Attitude control is achieved by a relative shift between the craft's center of pressure and its center of mass. This can be achieved with control vanes, movement of individual sails, movement of a control mass, or altering reflectivity.

Holding a constant attitude requires that the ACS maintain a net torque of zero on the craft. The total force and torque on a sail, or set of sails, is not constant along a trajectory. The force changes with solar distance and sail angle, which changes the billow in the sail and deflects some elements of the supporting structure, resulting in changes in the sail force and torque.

Sail temperature also changes with solar distance and sail angle, which changes sail dimensions. The radiant heat from the sail changes the temperature of the supporting structure. Both factors affect total force and torque.

To hold the desired attitude the ACS must compensate for all of these changes.

Constraintsedit

In Earth orbit, solar pressure and drag pressure are typically equal at an altitude of about 800 km, which means that a sail craft would have to operate above that altitude. Sail craft must operate in orbits where their turn rates are compatible with the orbits, which is generally a concern only for spinning disk configurations.

Sail operating temperatures are a function of solar distance, sail angle, reflectivity, and front and back emissivities. A sail can be used only where its temperature is kept within its material limits. Generally, a sail can be used rather close to the Sun, around 0.25 AU, or even closer if carefully designed for those conditions.

Comments

Post a Comment

Popular posts from this blog

Electric solar wind sail

Image
Pekka Janhunen from FMI has invented a type of solar sail called the electric solar wind sail. Mechanically it has little in common with the traditional solar sail design. The sails are replaced with straightened conducting tethers (wires) placed radially around the host ship. The wires are electrically charged to create an electric field around the wires. The electric field extends a few tens of metres into the plasma of the surrounding solar wind. The solar electrons are reflected by the electric field (like the photons on a traditional solar sail). The radius of the sail is from the electric field rather than the actual wire itself, making the sail lighter. The craft can also be steered by regulating the electric charge of the wires. A practical electric sail would have 50–100 straightened wires with a length of about 20 km each. citation needed Electric solar wind sails can adjust their electrostatic fields and sail attitudes.
Read more

Sail configurations

Image
IKAROS, launched in 2010, was the first practical solar sail vehicle. As of 2015, it was still under thrust, proving the practicality of a solar sail for long-duration missions. It is spin-deployed, with tip-masses in the corners of its square sail. The sail is made of thin polyimide film, coated with evaporated aluminium. It steers with electrically-controlled liquid crystal panels. The sail slowly spins, and these panels turn on and off to control the attitude of the vehicle. When on, they diffuse light, reducing the momentum transfer to that part of the sail. When off, the sail reflects more light, transferring more momentum. In that way, they turn the sail. Thin-film solar cells are also integrated into the sail, powering the spacecraft. The design is very reliable, because spin deployment, which is preferable for large sails, simplified the mechanisms to unfold the sail and the LCD panels have no moving parts. Parachutes have very low mass, but a parachute is not a worka...
Read more

History of concept

Image
Johannes Kepler observed that comet tails point away from the Sun and suggested that the Sun caused the effect. In a letter to Galileo in 1610, he wrote, "Provide ships or sails adapted to the heavenly breezes, and there will be some who will brave even that void." He might have had the comet tail phenomenon in mind when he wrote those words, although his publications on comet tails came several years later. James Clerk Maxwell, in 1861–1864, published his theory of electromagnetic fields and radiation, which shows that light has momentum and thus can exert pressure on objects. Maxwell's equations provide the theoretical foundation for sailing with light pressure. So by 1864, the physics community and beyond knew sunlight carried momentum that would exert a pressure on objects. Jules Verne, in From the Earth to the Moon , published in 1865, wrote "there will some day appear velocities far greater than these of the planets and the projectile, of which light or electri...
Read more